算符优先算法介绍

Posted on |

基于之前博文对java虚拟机栈的介绍，相信多数同学会想深入了解操作数栈是如何处理复杂运算的。接触过编译原理的应该对算符优先文法，逆波兰表达式（后缀表达式），中缀表达式这些定义不陌生。本篇文章主要介绍算符优先算法是如何通过栈进行复杂运算的。

中缀表达式

中缀表达式即我们输入的需要被计算的一个字符串，这里以四则运算为例：a-b*c+(d+e)/f,根据算符优先算法主要有以下几个数据结构：

  • 算法优先级数组（Optr Array）:存储算符优先级的列表，决定什么时候进行操作数和算符的入栈出栈。
  • 操作数栈（Opnd）：存储操作数，从表达式的左侧开始和算符栈一起扫描入栈出栈。
  • 算符栈（Optr）：存储算符，四则运算主要有+，-，*，/四种，外加（，）以及默认的最小优先级的#。

四则运算算符优先表

算符优先表可以看成一个二维数组，这里的关系为行元素+算符+列元素，如第一行+>+。这里可能有点歧义，为什么算符优先表会是一个二维数组，两个同样的算符还会出现优先级。需要强调的是在表达式扫描的过程中，首先出现的+算符优先级是要高于后出现的+的，所以我们需要明确算符优先表的概念是动态和具有顺序性的，我们看到的表也是具有一定的对称性。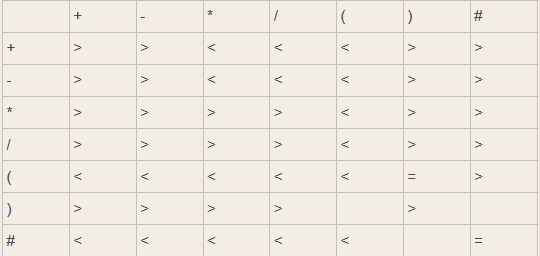
cmd-markdown-logo

中缀表达式计算四则运算

这里我们以a-b*c+(d+e)/f四则运算为例，演示算法的三部分是如何去保证计算输出正确结果的。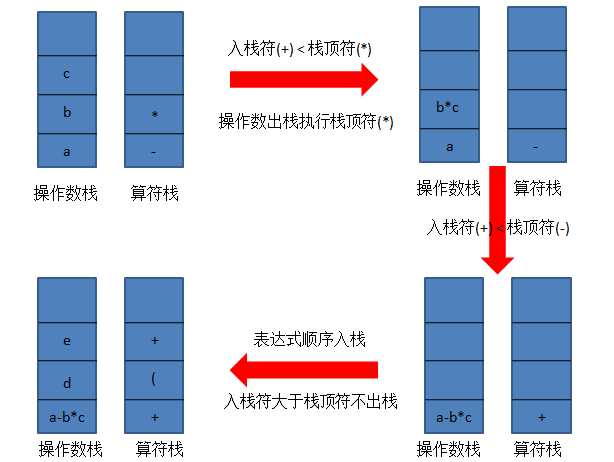
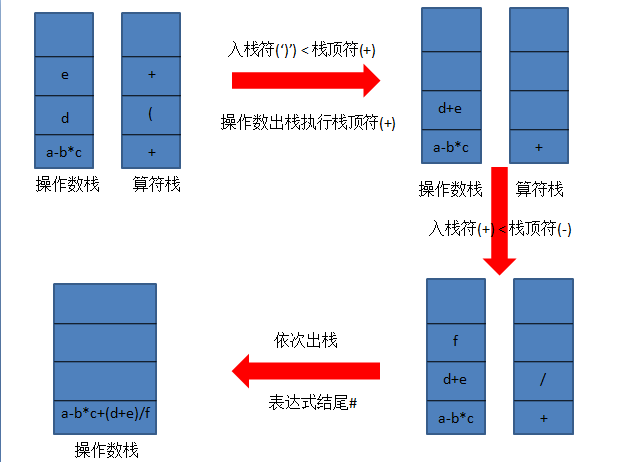
cmd-markdown-logo
cmd-markdown-logo

后缀表达式

后缀表达式又称为逆波兰表达式，逆波兰表达式是中缀表达式的简化版，为什么这么说，因为中缀表达式在计算过程中需要参考算符优先表。后缀表达式只需要建立操作数栈和算符栈直接按顺序入栈出栈即可得到表达式的结果。

后缀表达式计算

这里以a-bc+(d+e)/f四则运算为例，我们可以得到逆波兰表达式为abc*-de++f/，转化为逆波兰表达式之后对程序而言只需要从左向右扫描遇到算符即将左边的两个操作数直接以算符操作即可，十分易于理解。

中缀表达式转后缀表达式

中缀表达式a+bc+(de+f)g，其转换成后缀表达式则为abc +de f +g * +。
转换过程需要用到栈，具体过程如下：

  • 1）如果遇到操作数，我们就直接将其输出。
  • 2）如果遇到操作符，则我们将其放入到栈中，遇到左括号时我们也将 其放入栈中。
  • 3）如果遇到一个右括号，则将栈元素弹出，将弹出的操作符输出直到遇到左括号为止。注意，左括号只弹出并不输出。
  • 4）如果遇到任何其他的操作符，如（“+”， “*”，“（”）等，从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后，才将遇到的操作符压入到栈中。有一点需要注意，只有在遇到” ) “的情况下我们才弹出” ( “，其他情况我们都不会弹出” ( “。
  • 5）如果我们读到了输入的末尾，则将栈中所有元素依次弹出。

代码（中缀表达式）

可以通过中缀表达式利用算符优先表，操作数+算符栈计算结果。可以参考leetCode部分题解。这里附上leetCode P224 Basic Calculator AC代码。参考博文，https://www.cnblogs.com/zabery/archive/2010/08/11/1797602.html。

leetCode经典应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
package Stack.P224;

import java.util.Stack;

/**
 * Example 1:
 *
 * Input: "1 + 1"
 * Output: 2
 * Example 2:
 *
 * Input: " 2-1 + 2 "
 * Output: 3
 * Example 3:
 *
 * Input: "(1+(4+5+2)-3)+(6+8)"
 * Output: 23
 */
class Solution {
    //定义算符优先表 这里一共四种运算符号
    private String operators="()+-#";
    //定义算符优先级 二位数组
    private char[][] operatorArray=
            {{'<','=','<','<','>'},
            {'>',' ','>','>','>'},
            {'<','>','>','>','>'},
            {'<','>','>','>','>'},
            {'<',' ','<','<','='}};
    private boolean flag=false;//标记前面是否出现过数字
    public int calculate(String s) {
        //定义符号栈+数值栈
        Stack<Character> operator = new Stack<>();
        Stack<Integer> number = new Stack<>();

        //算符栈#作为结束符
        operator.push('#');
        s=s.concat("#");
        //循环
        Integer temp = 0;
        int index=0;
        Character cur=s.charAt(index);

        while (cur!='#' || operator.peek()!='#'){
            if (cur==' ') {
                cur=s.charAt(++index);
            }else if (cur>='0' && cur<='9'){
                temp = temp * 10 + cur - '0';
                flag=true;
                cur=s.charAt(++index);
            }else {
                if (flag) {number.push(temp);temp=0;flag=false;}
                switch (preCode(operator.peek(),cur)){
                    //当前运算符优先级较大，则直接入栈，置于栈顶(优先级高需先计算
                    case '<': operator.push(cur);cur=s.charAt(++index);break;
                    //弹出左括号
                    case '=': operator.pop();cur=s.charAt(++index);break;
                    //进行操作符运算
                    case '>': operator(number,operator.pop());break;
                }
            }
        }
        if (flag==true) {number.push(temp);}
        return number.pop();
    }

    private void operator(Stack<Integer> digitStack, Character cur) {
        //循环pop操作符和数值符 开始运算
        Integer second=digitStack.pop();
        Integer first=digitStack.pop();
        if (cur=='+') {
            digitStack.push(first+second);
        }else {
            digitStack.push(first-second);
        }
    }
    private char preCode(char first,char second){
        return operatorArray[operators.indexOf(first)][operators.indexOf(second)];
    }
    public static void main(String[] args) {
        System.out.println(new Solution().calculate("1 + 1"));
        System.out.println(new Solution().calculate("0"));
        System.out.println(new Solution().calculate("(1+(4+5+2)-3)+(6+8)"));
        System.out.println(new Solution().calculate("(7)-(0)+(4)"));
        System.out.println(new Solution().calculate(" 2-1 + 2 "));
    }
}

标准模版（针对所有运算）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/// <summary>
/// 算符优先算法
/// </summary>
/// <param name="infixExpression">中缀表达式</param>
/// <returns></returns>
public int ComputeExpression(string infixExpression)
{
    Stack<int> stackOperand = new Stack<int>();  //操作数栈
    Stack<char> stackOperator = new Stack<char>(); //操作符栈
    stackOperator.Push('#');  //作为栈空的结束符
    infixExpression = infixExpression + "#"; //中缀表达式的结束符
    int temp = 0;
    int result = 0;
    int count = 0;

    char cur = infixExpression[count];
    
    while (cur != '#' || stackOperator.Peek() != '#') //扫描完算术表达式，并且操作符栈为空
    {
        if (cur == ' ') continue;
        if (IsOperand(cur)) //操作数直接入栈
        {
            stackOperand.Push(Int32.Parse(cur.ToString()));
            cur = infixExpression[++count]; //扫描算术表达式下一位
        }
        else
        {
            switch (Precede(stackOperator.Peek(), cur)) //比较操作符栈顶元素和扫描的当前算符的优先级
            {
                    //当前运算符优先级较大，则直接入栈，置于栈顶(优先级高需先计算)
                case '<':
                    stackOperator.Push(cur);
                    cur = infixExpression[++count];
                    break;
                    //等于则表示栈顶元素为左括号，当前字符为右括号
                case '=':
                    stackOperator.Pop();//弹出左括号
                    cur = infixExpression[++count];
                    break;
                    //当前运算符优先级小，则弹出栈顶运算符并从操作数栈弹出两个操作数
                case '>':
                    temp = stackOperand.Pop();
                    result = stackOperand.Pop();
                    //注意计算的顺序，计算结果入操作数栈，并且继续比较新的栈顶操作符和当前操作符的优先级
                    stackOperand.Push(Operate(result, temp, stackOperator.Pop()));
                    break;
            }
        }
    }
    
    return stackOperand.Peek();
}

总结

为了加强之前的java运行时数据区域中提到的操作数栈的理解，也是着重介绍了算符优先算法，如何通过算符栈，优先表，操作数栈协调工作计算中缀表达式。同样的算法过程也可以用于将中缀表达式转化为后缀表达式。其实虚拟机栈中子节码指令，局部变量表，操作数栈的执行过程也是可以类比的，只不过已经被虚拟机优化过。