动态规划是算法中比较重要的一课,是一种典型的空间换取时间的算法。通常是可以用分治法取考虑一个动态规划问题,用递归实现代码上看起来更加浅显易懂。但是基于递归的实现都是n2的复杂度,这样的复杂度在递归栈到达一定深度的时候会变的非常慢,并且有非常多的重复操作。动态规划致力于将这类递归问题,通过空间换取时间,用容器的方式记录递归结果,减少了重复递归,同时降低了时间复杂度。
最长子数组问题
找出一个数组的连续子数组的最大和。最先想到的solution应该是n2的两次遍历。但是这样的循环是非常耗时的。我们尝试用分治的方式去思考一个复杂的问题,这是算法设计过程中常用的思维。当我们考虑一个任意数组比如{10,-1,2,-4,3,-5,10},找出最长的子数组。可以先找出{10,-1,2,-4,3,-5}的最长子数组,那么我们可以得到一个数学函数公式(今天想偷个懒,明早去公司画一画):

递归
通常得出递归数学公式之后我们可以直接写出一个直观的递归程序。递归程序如下,这里需要维护一个Sum类,需要记录最长子数组的起始元素位置:
1 | package MaxSubArray; |
递归程序:
1 | public class MaxSubArray { |
动态规划(DP)
分析上面的递归程序,n2的效率+递归调用栈,空间和时间利用率都不高。我们通过动态规划进行优化,动态规划的精髓可以用空间去换取空间。
1 | public class MaxSubArray { |
斐波那契数列问题
斐波那契数列的性质可以得到如下的数学递推公式,同样,我们提供递归和动态规划两种实现方式,这里我们看一下递推的公式:
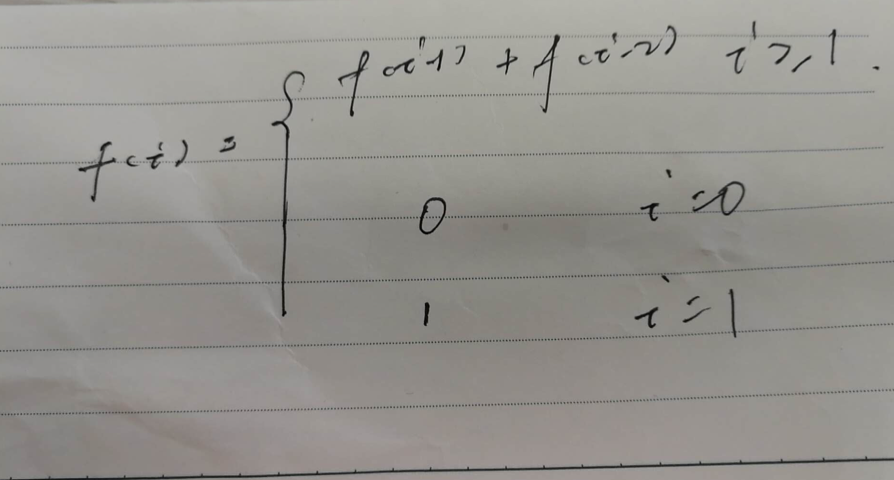
递归+DP
1 | package Fobi; |