Reverse Linked List

题目描述（难度简单）

Reverse a singly linked list.

Example:

Input: 1->2->3->4->5->NULL
Output: 5->4->3->2->1->NULL

Follow up:

A linked list can be reversed either iteratively or recursively. Could you implement both?

方法一：一遍遍历

一遍遍历，定义一个初始值为null的pre节点，一个current为head的当前节点，nextTemp为current的下一个节点。

首先定义好pre和current两个节点，中间虚线表示原来链表存在的指向，红色表示当前pre节点位置，绿色表示已经被倒转的节点，蓝色为待倒转节点：

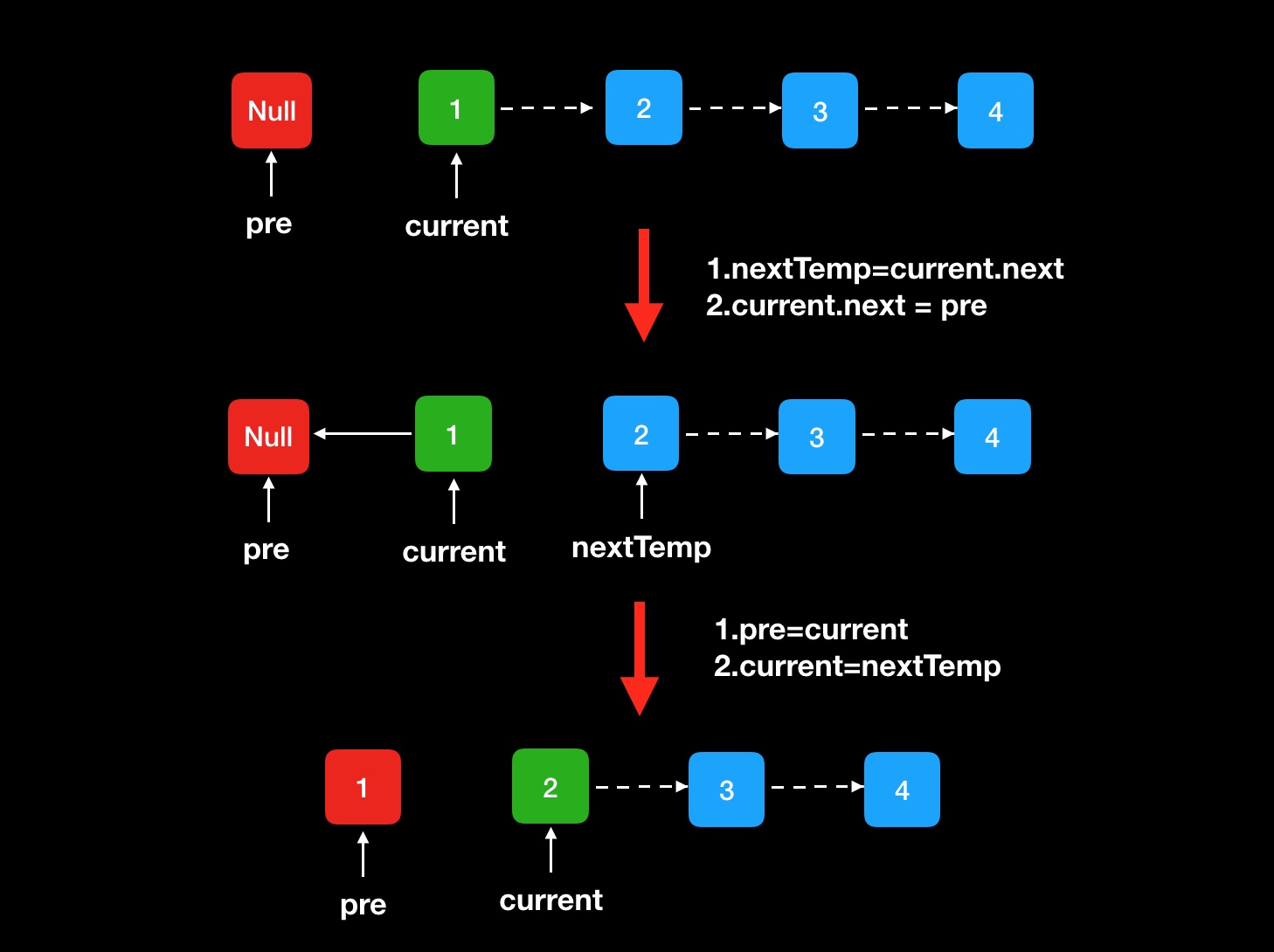
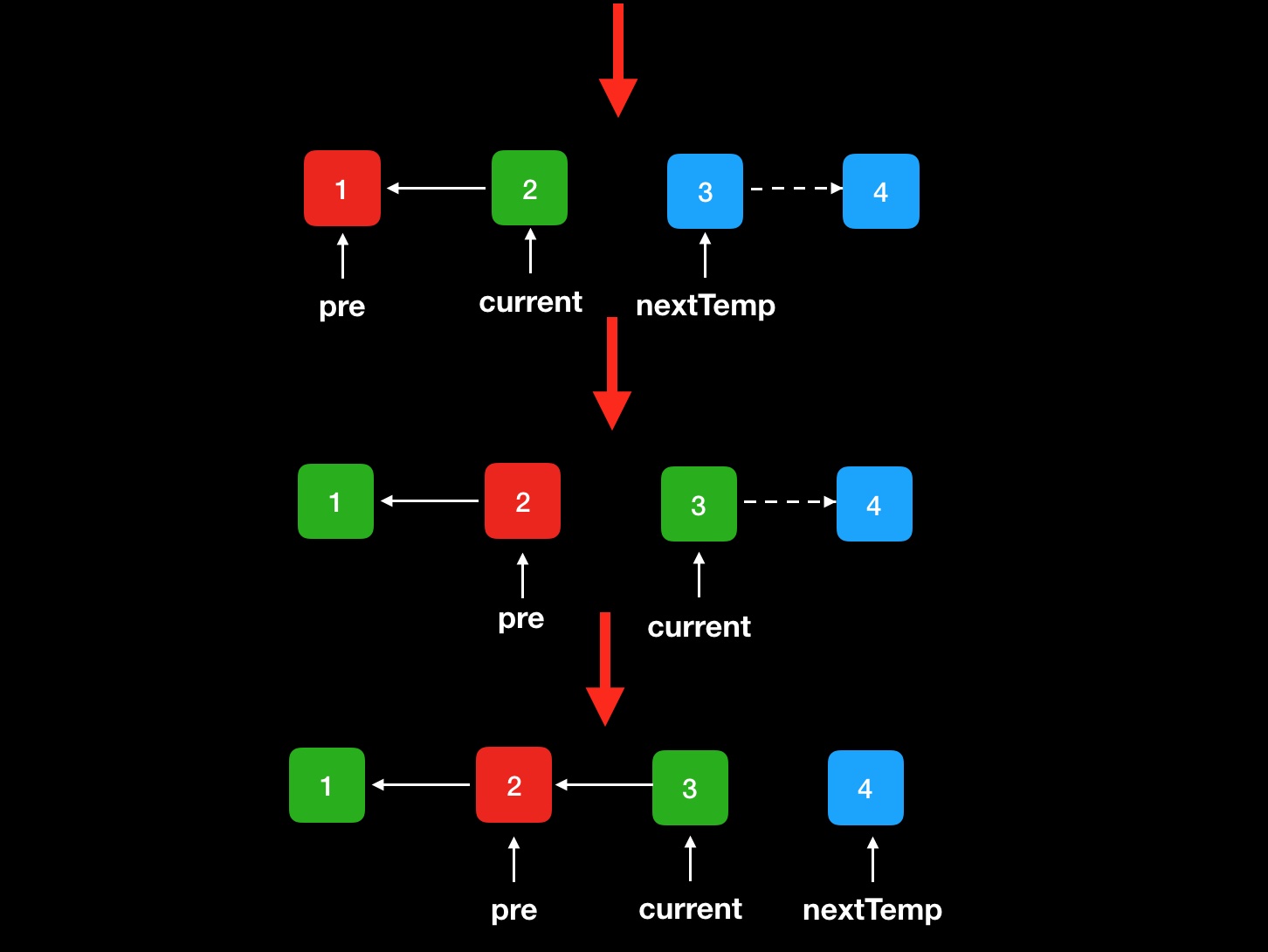
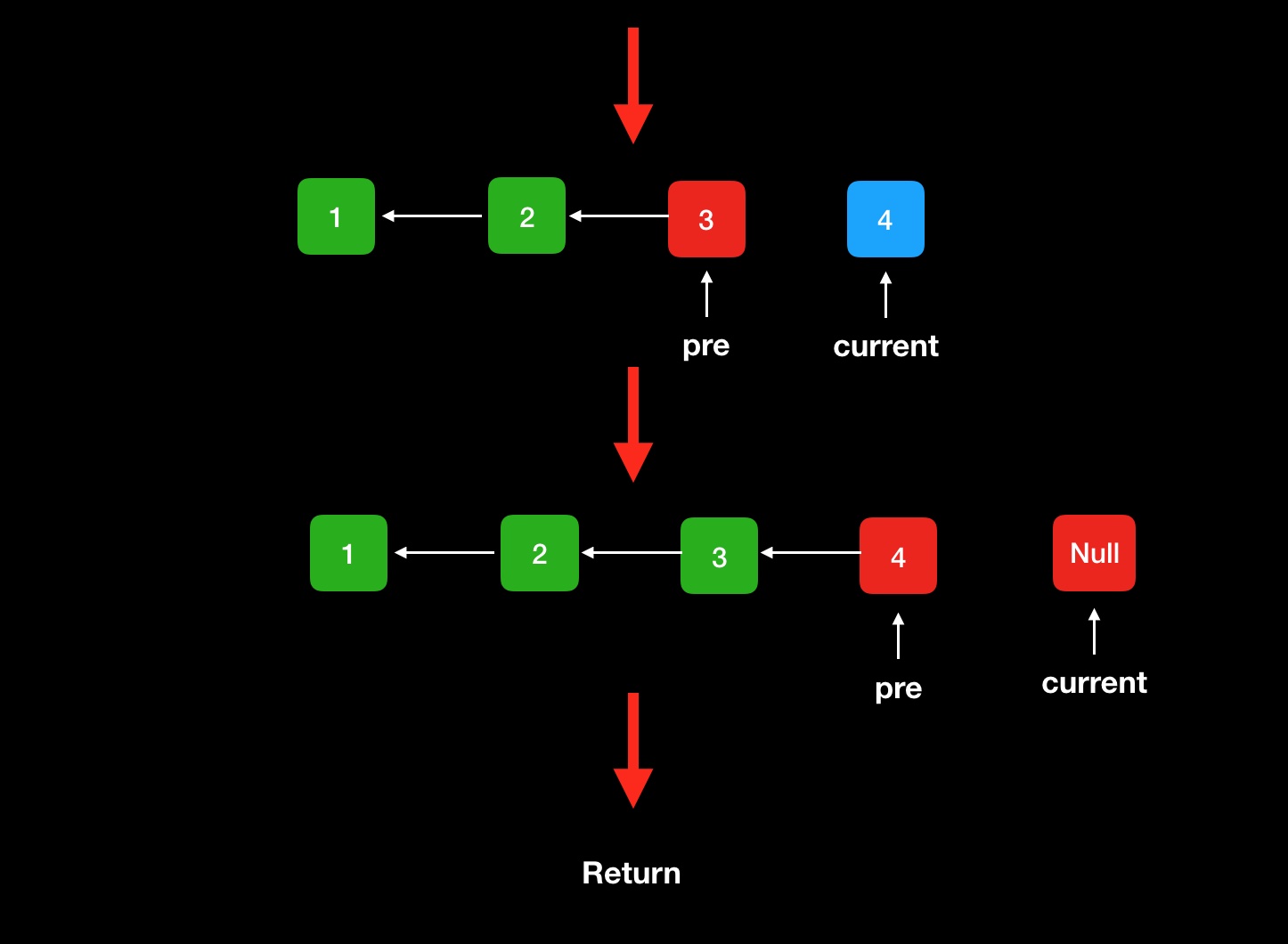
最后只需要pre返回也就完成了一次遍历。返回的链表也就是倒转之后的链表。

方法一代码：

在自己写的过程中发现代码并没有这么简洁，算法设计上没有这么完善，针对链表的题目还是需要画出来指向关系，写出优雅。这里循环结束的条件我们可以看到是current=null，然后直接返回pre。

public ListNode reverseListOneScanMoreClear(ListNode head){

    ListNode prev = null;
    ListNode curr = head;
    while (curr != null) {
        ListNode nextTemp = curr.next;
        curr.next = prev;
        prev = curr;
        curr = nextTemp;
    }
    return prev;
}

方法二：递归

递归的版本理解上较为复杂，因为如果递归到尾节点的时候，直接将尾节点返回作为倒转链表的头节点返回，这样的逻辑会有问题，我们总是需要在一次递归中寻找倒转链表的尾节点。当然我们可以通过记录链表最尾巴的节点作为头节点，然后每次递归返回当前倒转链表的尾节点，缺点就是丧失了递归的美感。这样的方式写出来的版本会是下面这样的，也比较好理解：

//记录倒转链表首节点
private ListNode newHead;

/**
* method 1 : 利用递归进行反转
* 递归返回的节点每次都是尾节点可以直接追加
* @param head
* @return
*/
public ListNode reverseList(ListNode head){
    reverseToTail(head);
    return this.newHead;
}
public ListNode reverseToTail(ListNode node){
    if(node == null || node.next==null){
        this.newHead=node;
        return node;
    }else {
        ListNode tempListNode=reverseToTail(node.next);
        tempListNode.next=node;
        node.next =null;
        return node;
    }
}

那么我们想能不能每次都返回倒转链表的头部然后不需要遍历到尾节点还能进行追加？我们假设在第三次递归返回的程序体中，后两个节点已经具备了倒转结构并且返回了头节点，也就是n1->n2->n3…n(k)->n(k+1)<-n(k+2)需要把n(k)节点在第三次递归中追加到倒转链表中。

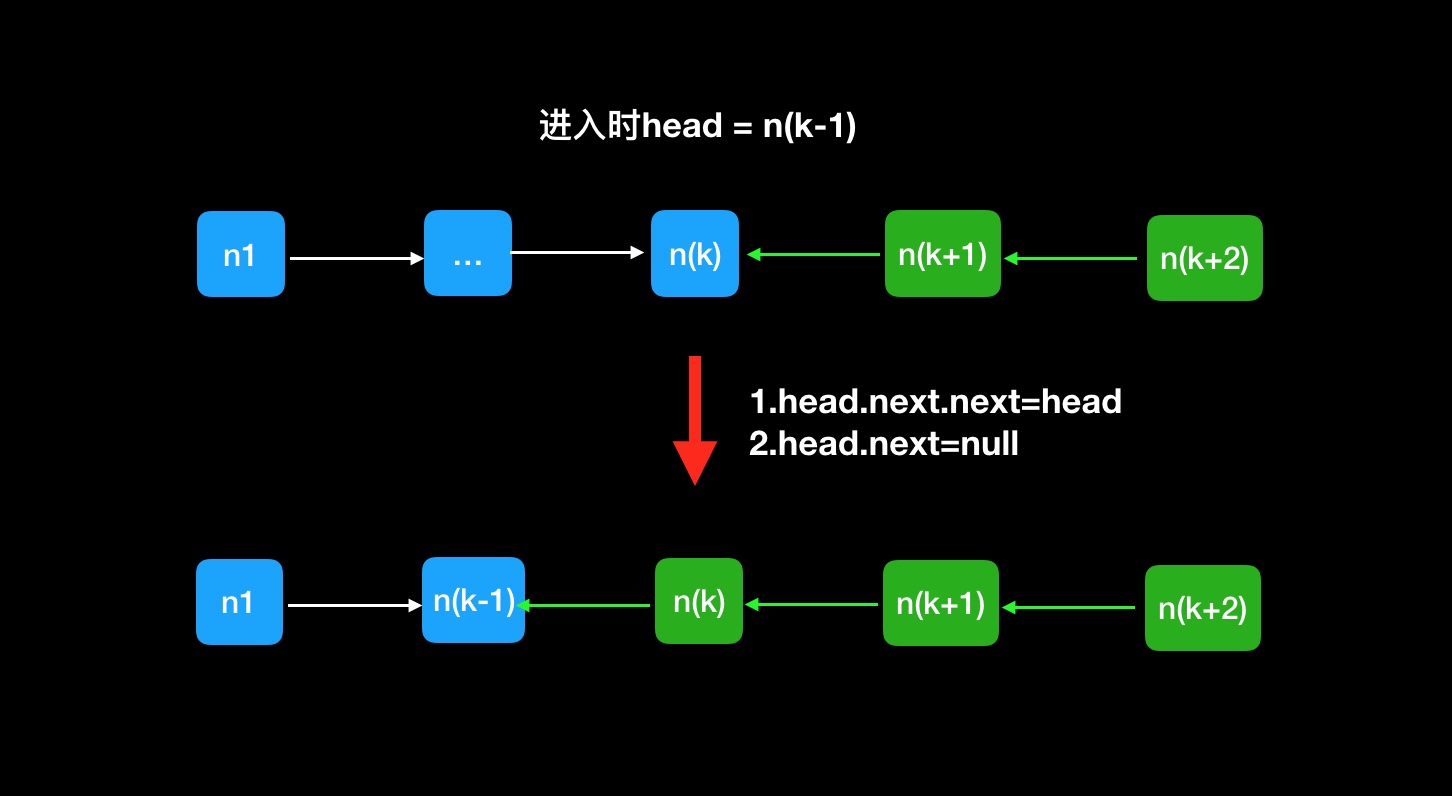
方法二代码：

public ListNode reverseList(ListNode head) {
    //1.recursion terminater
    if (head == null || head.next == null) return head;
    //2.drill down
    ListNode p = reverseList(head.next);
    //3.reverse the current level status if needed
    head.next.next = head;
    head.next = null;
    return p;
}

递归确实还是简洁，根据递归的范式写出来即可。

总结

链表倒转，主要可以通过一遍遍历和递归的方式来进行实现，实现的过程主要需要关注指针的指向，在指针的操作过程中写出来演示效果会更好，搞清楚指向关系很重要，否则很容易造成逻辑错误。